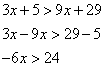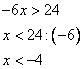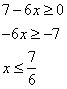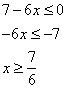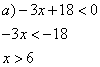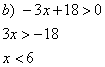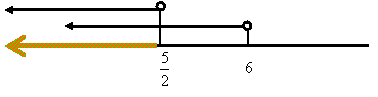Inecuaciones

Una inecuación es una operación cuyo resultado es un intervalo numérico. Las reglas a seguir para su resolución son, en principio, semejantes a las de las ecuaciones, pero se agregan otras reglas específicas para este tipo de operaciones.

Ejemplo 1

Primero resolvemos las operaciones de cada término.

Operamos

Despejamos x

Expresando como intervalo

                18

Ejemplo 2

Cuando la incógnita está multiplicada por un factor negativo, al pasarlo al otro miembro se debe invertir el sentido de la desigualdad.

Esto se debe a que

Entonces

                                           -4

Ejemplo 3

Cuando la incógnita figura en el denominador, debemos seguir los siguientes pasos.

1º) Igualamos a cero

2º) Sacamos común denominador

3º) Ahora debemos pensar:

• Tenemos un cociente cuyo resultado debe ser 0 o positivo. Por la regla de los signos en la división, el numerador y el denominador deben tener el mismo signo, es decir, que deben ser ambos positivos o ambos negativos
• El denominador no puede ser cero.

Entonces tenemos dos opciones

Resolvemos la primera

Como deben cumplirse las dos condiciones, la solución de la opción a) es la intersección de los dos intervalos obtenidos

 
                    1/2                                  7/6

Ahora hacemos lo mismo con la opción b)

En este  caso la intersección es nula, ya que no hay ningún número que cumpla simultáneamente con las dos condiciones (ser menor que 1/2 y mayor que 7/6)

Veamos otro ejemplo

Igualamos a cero y sacamos común denominador.

En este caso el resultado de este cociente debe ser negativo. De acuerdo con la regla de los signos el numerador y el denominador deben tener signos opuestos.

Resolvemos ambos opciones

El resultado final es la unión de estos intervalos