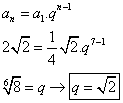|
 |
Una sucesión es un conjunto ordenado de términos en el que puede establecerse una correspondencia entre los elementos de la sucesión y la sucesión de números naturales. |
|
|
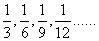
Podemos simbolizar esta sucesión como

|
Esto significa que cada término de la sucesión de obtiene reemplazando n por la sucesión de números naturales. |
Hay dos tipos de sucesiones especiales:
En las sucesiones aritméticas cada término se obtiene sumándole al anterior una cifra fija denominada “razón” o “diferencia”.
7, 10, 13, 16, 19…
En esta sucesión cada término se obtiene sumándole 3 al anterior.
Los elementos de la sucesión son:
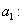 primer término (en nuestro caso, 7) primer término (en nuestro caso, 7)
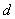 : diferencia o razón (3 en este ejemplo) : diferencia o razón (3 en este ejemplo)
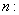 número de términos número de términos
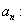 término enésimo. término enésimo.
La fórmula para obtener cualquier término de la sucesión es:
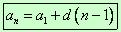
|
 |
Por ejemplo, si en la sucesión que pusimos como ejemplo queremos calcular el vigésimo término. |
|
|

En este tipo de sucesiones, cada término se obtiene al multiplicar el anterior por una cifra fija denominada “razón”

En este caso cada término se obtiene multiplicando al anterior por 4.
La fórmula para obtener cualquier término es:

Siendo q la razón de la sucesión.
Suma de términos
Para calcular la suma de los n primeros términos de una sucesión utilizamos las siguientes fórmulas:
Sucesiones aritméticas

Sucesiones geométricas

|
 |
Algunos ejemplos de resolución de ejercicios |
|
|
1) De una sucesión aritmética se conoce:

Calcular:
a) La razón.
b) La suma de los primeros 25 términos.
a) Escribimos la fórmula del término enésimo, y a partir de allí despejamos la razón:

b) Para calcular la suma de los primeros 25 términos, calculamos primero 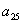 y luego la suma y luego la suma

2) En una sucesión aritmética el tercer término es -2 y el séptimo término es 18. Calcular la suma de los primeros 11 términos.
Nuestros datos son:

Para calcular la diferencia, armaremos una “sub-sucesión”

Tomaremos al - 2 como primer término y al 18 como término quinto:

Entonces:

Ahora calculamos 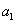 y y 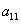 volviendo a la sucesión original. volviendo a la sucesión original.

3) En una sucesión geométrica 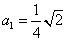 y y 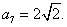 Calcular: Calcular:
a) La razón
b) la suma de los primeros 12 términos.
a)
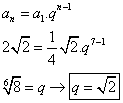
b)

4) En una sucesión geométrica 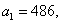 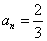 y y 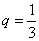 . Calcular el número de términos. . Calcular el número de términos.
A partir de la fórmula del término enésimo debemos despejar n.

|
 |
84) El alquiler de un auto cuesta $420 el primer día y $250 cada uno de los días subsiguientes.
a) ¿Cuál es el costo de 16 días de alquiler?
b) Si se abonaron $3170 ¿durante cuánto tiempo se alquiló el automóvil?
85) En una sucesión aritmética de 12 términos, el primero es 8 y la suma de todos los términos es -36. Calcular la diferencia.
86) Calcular el décimo término de una sucesión aritmética cuyo segundo y cuarto término son, respectivamente, 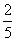 y 1. y 1.
87) Calcular el séptimo término de una sucesión geométrica de razón positiva que tiene por tercero y quinto término, respectivamente, 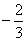 y -6. y -6.
88) En una programación geométrica de 11 términos y razón 2, la suma de todos los términos es 4094. Calcular el primer término.
89) En una sucesión geométrica de 7 términos, el primero es 6000 y el último 0,006. Calcular la suma de todos los términos.
90) Seis hermanos reciben un legado. El mayor recibe $320.000 el segundo $480.000 y así sucesivamente en sucesión geométrica. ¿Cuántos de ellos se vuelven millonarios gracias a la herencia?
91) En una sucesión geométrica 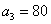 y y 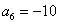 . Calcular la suma de los primero 5 términos. . Calcular la suma de los primero 5 términos.
92) Un banco ofrece el 2% de interés mensual para depósitos a plazo fijo de 30 días. Si se depositan $50.000, y llamamos Mn al monto obtenido luego de n meses:
a) Calcular: i) M8 ii) Mn
b) Comprobar que Mn es una progresión geométrica y calcular su razón
c) ¿Cuántos meses debe estar depositado el dinero para obtener un monto superior a $90.000? |
|
|
|