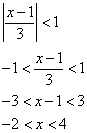Series de Potencias

Una serie de funciones es una serie cuyos términos, en vez de ser números, son funciones escalares.

Dentro de las series de funciones, un caso particular es el de la series de potencias que pueden simbolizarse como

        con  y x variable.

Intervalo de convergencia de una serie de potencias

El intervalo de convergencia es el conjunto de números reales para los cuales la serie de potencias converge.

Ejemplo

Hallar el intervalo de convergencia de la serie de potencias

Aplicamos el criterio de D’ Alembert:

De acuerdo con el criterio de D’ Alembert, para que la serie converja debe cumplirse que , entonces

El intervalo de convergencia es (-2,4).

Para saber si el intervalo de convergencia incluye a los extremos, debemos analizar el comportamiento de la serie para  y para .

Si

Para , la serie es alternada, entonces para analizarla debemos utilizar el criterio de Leibniz.

Primero analizamos el crecimiento.

Como n es un número natural, es siempre positivo, por lo tanto nunca se cumple la condición expresada en la inecuación.

La serie no es decreciente, por lo tanto para  diverge.

Para

Esta serie puede escribirse como

Es una serie armónica generalizada de exponente menor a 1, por lo tanto diverge.

Entonces nuestra serie de potencias tiene como intervalo de convergencia

Radio de Convergencia

El radio de convergencia es el intervalo que se extiende entre el centro del intervalo de convergencia y uno de sus extremos.

En el ejemplo dado, el radio de convergencia es 3:

100) Hallar el intervalo y el radio de convergencia de las siguientes series potencias. a) b) c) d) e) f) g) h)