|
 |
Podemos definir a una serie numérica como la suma de los términos de una sucesión. |
|
|
Clasificación de las series
|
Series convergentes
Una serie es convergente cuando la suma de sus términos tiende a un valor finito. |
|
Series divergentes
Una serie es divergente cuando la suma de sus términos tiende a infinito. |
|
Series oscilantes
Una serie es oscilante cuando la suma de sus términos no tiende a un valor único. |
Condición necesaria de convergencia
Si la serie 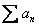 converge, entonces:
Esta es una condición necesaria pero no suficiente.
|
Es decir que si el límite es distinto de cero, la serie diverge, pero si el límite es igual a cero, no podemos afirmar nada. |
Para saber si la serie efectivamente converge, debemos probarlo mediante alguno de los criterios de convergencia.
|
Inicio
